1. Transition Temperature*(T_g)

The glass transition temperature T_g refers to the temperature at which the glass transforms from a lower temperature glassy state to a higher temperature super-cooled liquid state. This behavior shows thermal expansion measurement as a function of temperature. For this measurement, the test specimen is heated at a constant rate of 4°C/min. A differential thermal dilatometer is used for the measurement, as it maintains a uniform temperature distribution within the furnace to ±1°C. The glass transformation temperature is defined as the intersection of two lines that are extrapolated from the low and high temperature sides, respectively, of this curve,in fig 5. For the high-temperature line, we consider the values at which the gradient is the highest. For the low-temperature line, we determine a value 150°C below T_g. The unit for T_g is °C. The glass viscosity at T_s corresponds to about 10¹³-10¹⁴ dPa • s. T_g serves as a useful benchmark for annealing.

Notes
1dPa • s = 1poise

Fig. 5 Thermal Expansion Curve

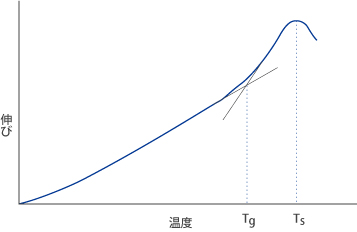
2. Sag Temperature (T_s)

The sag temperature, T_s, is defined as the temperature at which thermal expansion1 stops** increasing and actually begins to decrease. The viscosity of the glass at T_s corresponds to about 10¹⁰-10¹¹dPa • s.

**This phenomenon does not demonstrate the thermal expansion property essential to glass. That occurs as a deformation caused by the load applied to the glass specimen and the dead weight of the glass.

3. Coefficient of Thermal Expansion* (α)

The coefficient of thermal expansion is indicated by α_n (for the normal temperature range : -30°C - +70°C) and α_h (for the high temperature range: +100°C - +300°C), respectively, and expressed by 10^-7/°C. An interference-dilatometer for α_n and a differential thermal dilatometer for α_h are used as measurement instruments. The coefficient of thermal expansion α_n and α_h are obtained by the next formula.

Where, dT_n is temperature difference of -30 - 70°C (K), L is the initial length of the sample (mm) and dL_n is the amount (mm) of the change of the sample length from -30°C - 70°C.

Where, dT_h is temperature differenceof 100 - 300°C (K), L is the initial length of the sample (mm) and dL_h is the amount (mm) of the change of the sample length from 100°C - 300°C.

4. Strain Point (T₁₀^14.5)

The strain point, T10^14.5, represents a temperature at which internal stresses in a glass are relieved after a few hours. The viscosity of the glass at that temperature corresponds to about 10^14.5dPa•s.

It is measured by the method of regulations by JIS R3103-02:2001.

5. Annealing Point (T₁₀¹³)

The annealing point, T10¹³, represents a temperature at which internal stresses in a glass are relieved after a few minutes. The viscosity of the glass at that temperature corresponds to about 10¹³dPa•s.

It is measured by the method of regulations by JIS R3103-02:2001.

6. Softening Point (T₁₀^7.6)

It is thought to be the temperature** equivalent to a viscosity of about 10^7.6 dPa•s where the glass starts to soften remarkably under its own weight.

Notes ** :
Also known as the Littleton Point.
It is measured by the method of regulations by JIS R3103 -1:2001

7. Coefficient of Thermal Conductivity (λ)

The coefficient of thermal conductivity (λ) is a value in which the heat flow rate density (heat flow velocity) is divided by the temperature gradient. That is, the calorie that moves through the unit area at the unit time is divided by temperatures difference for each unit distance It is shown it by the unit of W / (m • K).

Note:
W / (m • K) = 8.6000×10^-1kcal / (h • m•°C) = 2.38889×10^-3cal / (s • cm • °C)
The coefficient of thermal conductivity is measured by the method of applying to JIS R1611:2010,

8. Specific Heat(specific heat capacity) (C_p)

Specific heat (C_p) is a value in which thermal capacity is divided by mass. That is, the calorie that requires it to raise the temperature of the material of the unit mass at 1°C. It is shown by the unit of kJ/(kg•K).

Note:
1kJ / (kg • K) = 2.3889 × 10^-1cal / (g • °C)
The specific heat capacity is measured by the method of applying to JIS R1611:2010