1. Refractive Index*
The refractive index is defined as the ratio of the phase velocity of light in air and glass. The refractive index of optical glass is measured using 15 spectral lines in table 2.
Table2 Wavelengths of Spectral Lines for Determining Refractive Indices| Wavelength (nm) | Spectral Line | Element |
|---|---|---|
| 1,013.98 | t線(赤外水銀) | Hg |
| 852.11 | s線(赤外セシウム) | Cs |
| 768.195 | A'線(赤色カリウム) | K |
| 706.519 | r線(赤色ヘリウム) | He |
| 656.273 | C線(赤色水素) | H |
| 643.847 | C'線(赤色カドミウム) | Cd |
| 632.8 | (632.8)(He-Neレ-ザ-) | He-Neレ-ザ- |
| 589.294 | D線(黄色ナトリウム) | Na |
| 587.562 | d線(黄色ヘリウム) | He |
| 546.074 | e線(緑色水銀) | Hg |
| 486.133 | F線(青色水素) | H |
| 479.991 | F'線(青色カドミウム) | Cd |
| 435.834 | g線(青色水銀) | Hg |
| 404.656 | h線(紫色水銀) | Hg |
| 365.015 | i線(紫外水銀) | Hg |
When the refractive index is shown in six digits, the seventh digit is rounded down. When the refractive index is shown in five digits, the sixth digit is rounded off.
2. Dispersion Formula
The refractive index at a wavelength can be calculated from a dispersion formula. For practical approximation, the following dispersion formula, derived from a series expansion of the theoretical formula, is available:
n2 = A0+A1λ2+A2λ-2+A3λ-4+A4λ-6+A5λ-8
where λ is the wavelength in μm.A0, A1,A... A5 are coefficients to be determined in each glass, using the method of least squares. The accuracy of a calculated refractive index at a wavelength between the range of 365 - 1014nm is ± 5 × 10-6 for typical glass with refractive indices.
3. Dispersion* and Abbe-number*
Dispersion is a phenomenon in which the refractive index depends on the wavelength. Generally, the refractive index of a long wavelength is smaller than that of a short wavelength to light. The Abbe number is used as the value showing dispersion properties. Additionally, dispersion is listed as nF - nC and nF'- nC' to six decimal places.
The Abbe-numbers,νd and νe, are respectively determined using the following formulas:
![]()
Refractive indices with six decimal places are used in the calculation. The numerical value of νd and νe are rounded off to two and Three decimal places.
4. Partial Dispersion Ratio
The relative partial dispersion Px,y and the alternate relative partial dispersion P'x,y are defined by the following equation:
![]()
Partial dispersion ratio is usually shown as the calculated value for a particular spectral range. In this catalog, for the often-used Pd_c , Pg_F,P'd_c' ,P' g_F'.
Refractive indices with six decimal places are used in the calculation. The numerical value of Px,y and P'x,y are rounded off to four decimal places.
5. Abnormal Dispersion
The dispersive characteristics of various glasses may be compared by plotting the relative partial dispersion Px,y versus the Abbe-number νd (or, alternatively, P'x,y versus νe). subscripts x and y denote the standard spectral line assignment associated with specific refractive index values.
Px,y = ax,y+bx,y•νd
where, ax, y and bx,y are constants.
Glasses which deviate significantly from the line described by the normal dispersion glasses above are called "abnormal dispersion glasses" . For any glass, the deviation of the partial dispersion from the "normal line" can be represented by the quantity ΔPx,y. A more general expression for Px,y is then given by the following equation:
Px,y = ax,y + bx,y•νd + ΔPx,y
ΔPx,y values listed in this catalog are referenced to a straight line defined by the Px,y values found for the glass types C7 and F2. ΔPC_t and ΔPg_F and ΔPi_g for each glass type are presented herein.
Table3 Refractive Indices of C7 and F2
| Glass | C7 | F2 |
|---|---|---|
| Code | 511-605 | 620-363 |
| nd | 1.51112 | 1.62004 |
| νd | 60.49 | 36.30 |
| nF-nC | 0.008450 | 0.01708 |
| ne | 1.51314 | 1.62409 |
| νe | 60.25 | 36.05 |
| nF' - nC' | 0.008517 | 0.017314 |
| Refractive Index | ||
| nt | 1.50154 | 1.6028 |
| ns | 1.50395 | 1.60669 |
| nA' | 1.50558 | 1.60954 |
| nr | 1.50707 | 1.61225 |
| nC | 1.50854 | 1.61502 |
| nC' | 1.50895 | 1.61581 |
| n632.8 | 1.50934 | 1.61655 |
| nD | 1.51105 | 1.61989 |
| nd | 1.51112 | 1.62004 |
| ne | 1.51314 | 1.62409 |
| nF | 1.51699 | 1.63210 |
| nF' | 1.51747 | 1.63312 |
| ng | 1.52155 | 1.64206 |
| nh | 1.52532 | 1.65070 |
| ni | 1.53174 | 1.66631 |
| Coefficients of Dispersion Formula | ||
| A0 | 2.2513560 100 | 2.5528303 100 |
| A1 | -7.9494605 10-3 | -7.5325484 10-3 |
| A2 | 1.1616810 10-2 | 2.4129973 10-2 |
| A3 | 1.5150006 10-4 | 3.9503274 10-4 |
| A4 | -3.1524929 10-6 | 4.1244910 10-5 |
| A5 | 4.8412686 10-7 | 1.2463873 10-6 |
| Relative partial dispersion | ||
| PA'_t | 0.4782 | 0.3947 |
| Pr_A' | 0.1758 | 0.1586 |
| PC_r | 0.1745 | 0.1623 |
| Pd_C | 0.3054 | 0.2938 |
| Pe_d | 0.2387 | 0.2370 |
| PF_e | 0.4559 | 0.4692 |
| Pg_F | 0.5393 | 0.5829 |
| Ph_g | 0.4463 | 0.5061 |
| Pi_h | 0.7597 | 0.9139 |
| P'A'_t | 0.4744 | 0.3893 |
| P'r_A' | 0.1744 | 0.1564 |
| P'C'_r | 0.2214 | 0.2056 |
| P'd_C' | 0.2547 | 0.2444 |
| P'e_d | 0.2368 | 0.2338 |
| P'F'_e | 0.5085 | 0.5218 |
| P'g_F' | 0.4789 | 0.5161 |
| P'h_g | 0.4428 | 0.4993 |
| P'i_h | 0.7537 | 0.9015 |
6. Temperature Coefficient of Refractive Index* (dn/dT)
The refractive index of the optical glass changes depending on the temperature. The temperature coefficient of the refractive index, (dn/dT) abs is measured at 20° intervals between -40 to 150°C in a vacuum using an interference-dilatometer to detect changes in both optical path length and dilation of the specimen. (Based on JOGIS 18-1994)
Laser light with wavelengths of 405, 491, 632.8, and 786 nm was used. For calculation of the temperature coefficient of the relative refractive (dn/dT) rel. in air at 101.325 kPa, the following equation is given:
![]()
Where Δnair. / ΔT is the temperature coefficient of the refractive index of air. Reference should be made to the table.
Table4 Temperature coefficient of refractive index of air
| Temp. (℃) |
Δnair./ΔT(10-6/K) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A' | r | C | C' | He-Ne | d | e | F | F' | g | h | |
| 768.19 | 706.52 | 656.27 | 643.85 | 632.8 | 587.56 | 546.07 | 486.14 | 479.99 | 435.835 | 404.66 | |
| -40/-20 | -1.35 | -1.35 | -1.35 | -1.35 | -1.35 | -1.36 | -1.36 | -1.37 | -1.37 | -1.38 | -1.38 |
| -20/0 | -1.15 | -1.15 | -1.15 | -1.16 | -1.16 | -1.16 | -1.16 | -1.17 | -1.17 | -1.17 | -1.18 |
| 0/20 | -0.99 | -1.00 | -1.00 | -1.00 | -1.00 | -1.00 | -1.00 | -1.01 | -1.01 | -1.01 | -1.02 |
| 20/40 | -0.87 | -0.87 | -0.87 | -0.87 | -0.87 | -0.87 | -0.88 | -0.88 | -0.88 | -0.89 | -0.89 |
| 40/60 | -0.76 | -0.76 | -0.77 | -0.77 | -0.77 | -0.77 | -0.77 | -0.77 | -0.77 | -0.78 | -0.78 |
| 60/80 | -0.68 | -0.68 | -0.68 | -0.68 | -0.68 | -0.68 | -0.68 | -0.69 | -0.69 | -0.69 | -0.69 |
| 80/100 | -0.60 | -0.60 | -0.61 | -0.61 | -0.61 | -0.61 | -0.61 | -0.61 | -0.61 | -0.62 | -0.62 |
| 100/120 | -0.54 | -0.54 | -0.54 | -0.54 | -0.54 | -0.55 | -0.55 | -0.55 | -0.55 | -0.55 | -0.56 |
| 120/140 | -0.49 | -0.49 | -0.49 | -0.49 | -0.49 | -0.49 | -0.49 | -0.50 | -0.50 | -0.50 | -0.50 |
| 140/150 | -0.46 | -0.46 | -0.46 | -0.46 | -0.46 | -0.46 | -0.46 | -0.46 | -0.46 | -0.46 | -0.47 |
Wavelength dependence of temperature coefficient of refractive index.
The relationship between the wavelength of light and the temperature coefficient of the absolute refractive index with respect to temperature is calculated by the following equation.
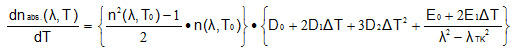
T0:Reference temperature (23℃)
n(λ,T0):Refractive index of light of wavelength λ at the reference temperature
dnabs.(λ,T)/dT:Temperature coefficient of absolute refractive index of light of
wavelength λ at temperature T
ΔT:Temperature difference(T-T0)
D0, D1, D2, E0, E1,λTK are constants specific to the glass type and are posted on the website Excel catalog. Moreover, dn / dT at each wavelength and each temperature obtained by this formula is posted on the homepage Excel catalog.
In this catalog, we showed the temperature coefficient (dνd / dT) of νd obtained from the temperature coefficient of nd and the temperature coefficient of nF and nC.
Expansion coefficient at each temperature
The expansion coefficient is shown as the average value in the high temperature range of 300 ~ 100 ℃ and the normal / low temperature range -30~70℃, The thermal expansion coefficients at -40~-20℃, 20~40℃, 80~100℃, which are necessary for finer temperature analysis, are posted.
The homepage is published in the Excel catalog at -40 ~ 150℃ at intervals of 20℃.
7. Temperature Coefficient of Optical Path Length(ds/dT)
The optical path length also changes with the temperature. The degree of the change is expressed as the "temperature coefficient of optical path length (ds/dT)" and is given by the following equation:
![]()
where n is the refractive index of the glass, α is the coefficient of linear thermal expansion of the glass, and dn/dT is the temperature coefficient of the refractive index of the glass.
In ordinary optical glass, the ds/dT is fairly large with a positive sign, as ds/dT is positive. Thus the optical path length will vary with the temperature to cause wave front distortion, which may present serious problems in high resolution optical systems.
The glasses with negative dn/dT, nearly zero ds/dT are called "Athermal Glasses".8. Stress Optical Coefficient (B)
When an optical glass is precisely annealled, it is isotropic and does not show optical birefingence. However, if power is added from the outside to the glass mechanically, or temperature fluctuation by heating and cooling, stress is induced in the glass A stressed optical glass is no longer isotropic and exhibits optical birefringence. When the optical path deviation caused by the birefringence is assumed to be δ(nm), the stress deviation caused in the glass is assumed to be σ(105Pa), and the thickness of the glass is assumed to be d(cm). The change in birefringence can be calculated by the following formula.
δ = B•σ•t
The B constant in the above formula is a dependend of the glass material, and it is called the opto-elastic constant. It is shown in the unit of 10-12/Pa.
In this catalog, the Stress Optical Coefficient is obtained by using a He-Ne laser light to measure the optical path deviation that exists at the center of the disc when the compressive load is vertically added to surface of the disk.
Notes
10-12 / Pa = 0.9807(nm / cm) / (kgf / cm2)
105Pa = 1.0197kgf / cm2
9. Coloration Code*
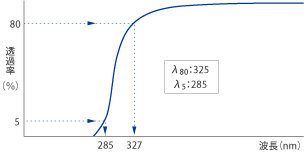
Optical glass exhibits almost no light absorption over a wavelength range extending from the visible to the near infra-red. The spectral transmittance characteristics of optical glass can be simply summarized with the coloration code λ80/λ5.
The coloration code is determined in the following way. The internal transmittance including surface reflection loss of a specimen with thickness 10±0.1mm is measured. Wavelengths are rounded off to the nearest 5nm. λ80 is the wavelength for which the glass exhibits 80% transmittance, while λ5 is the wavelength at which the glass exhibits 5% transmittance. For example, a glass with 80% transmittance at 327nm and 5% transmittance at 285nm has a coloration code of λ80=325,λ5=285.
Fig. 1 Designation of the Coloration Code with a Spectral Transmittance Curve
This catalog and later catalogs use a new coloration code for glass types with high refractive indexes for which ne≥1.85. The new coloration code is based on the wavelengths at which the glass exhibits transmission rates of 70% and 5%, respectively (λ70 / λ5) .
When we use λ70 to show coloration, the first half of the code is circled. For instance, (420).
10. Internal Transmittance* (τ)
The internal transmittance 'τ' refers to transmittance obtained by excluding reflection losses at the entrance and exit surfaces of the glass.
Internal transmittance values are calculated from transmittance measurement (τ) , including surface reflection losses on a pair of specimens with different thicknesses, and are given by a mathematical calculation.
In this catalog, the internal transmittance of 5mm and 10mm are shown as τ5mm and τ10mm, respectively, at wavelength between 280 - 1500nm
![]()
τ: Internal transmittance based on transmittance of samples thicknesses is 10mm
Δd: Different thickness of samples d2 - d1
T1 : Transmittance including surface reflection loss obtained by thickness d1 of the sample
T2 : Transmittance including surface reflection loss obtained by thickness d2 of the sample
Notes : d1>d2
11. Coloration of Internal Transmittance
In this catalog As a simple to measure the degree of coloration, The wavelength that internal transmittance ,equivalent to 80% is showed as λτ0.8.
12. Chromaticity
Chromaticity coordinate(X,Y) is described by using source of light D65 in accordance with JISZ8701 (Method of describing color by XYZ color system and X10Y10Z10 color system) and JISZ8722 (Measuring method of object color)
13. CCI
CCI (Color Contribution Index) shows the light transmission characteristics of each glass type using the method specified in ISO 6728 and JIS B 7097-1986.
Calculated using internal transmittance (wavelength range: 360~680 nm, wavelength spacing 10mm) of 10mm thick.
CCI (G), (R) was posted in this catalog.
For details, please refer to JIS 7097-1986 "ISO color characteristic index (ISO/CCI) for expressing color characteristics of lens for photography".





